Definicion y Representacion Grafica de una Funcion Cuadratica

Una función cuadrática es aquella que puede escribirse como una ecuación de la forma:

f(x) = ax 2 + bx + c

donde a , b y c (llamados términos ) son números reales cualesquiera y a es distinto de cero (puede ser mayor o menor que cero, pero no igual que cero). El valor de b y de c sí puede ser cero .

En la ecuación cuadrática cada uno de sus términos tiene un nombre.

Así,

ax 2 es el término cuadrático

bx es el término lineal

c es el término independiente

Cuando estudiamos la ecuación de segundo grado o cuadrática vimos que si la ecuación tiene todos los términos se dice que es una ecuación completa , si a la ecuación le falta el término lineal o el independiente se dice que la ecuación es incompleta .

Representación gráfica de una función cuadrática

Si pudiésemos representar en una gráfica "todos" los puntos [x,f(x)] de una función cuadrática , obtendríamos siempre una curva llamada parábola .

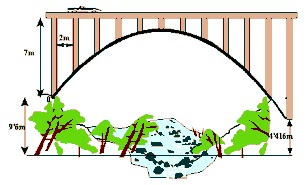
Parábola del puente, una función cuadrática.

Como contrapartida, diremos que una parábola es la representación gráfica de una función cuadrática .

Dicha parábola tendrá algunas características o elementos bien definidos dependiendo de los valores de la ecuación que la generan.

Estas características o elementos son:

Orientación o concavidad (ramas o brazos)

Puntos de corte con el eje de abscisas (raíces)

Punto de corte con el eje de ordenadas

Eje de simetría

Vértice

Orientación o concavidad

Una primera característica es la orientación o concavidad de la parábola. Hablamos de parábola cóncava si sus ramas o brazos se orientan hacia arriba y hablamos de parábola convexa si sus ramas o brazos se orientan hacia abajo.

Esta distinta orientación está definida por el valor (el signo) que tenga el término cuadrático (la ax ² ) :

Si  a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x ² − 3x − 5

Si  a < 0 (negativo) la parábola es convexa o con puntas hacia abajo, como en f(x) = −3x ² + 2x + 3

Además, cuanto mayor sea |a| (el valor absoluto de a), más cerrada es la parábola.

Puntos de corte en el eje de las abscisas (Raíces o soluciones) (eje de las X)

Otra característica o elemento fundamental para graficar una función cuadrática la da el valor o los valores que adquiera x , los cuales deben calcularse.

Ahora, para calcular las raíces (soluciones) de cualquier función cuadrática calculamos

f (x) = 0 .

Esto significa que las raíces (soluciones) de una función cuadrática son aquellos valores  de x para los cuales la expresión vale 0; es decir, los valores de x tales que y = 0 ; que es lo mismo que f(x) = 0 .

Entonces hacemos

ax² + bx +c = 0

Como la ecuación ax² + bx +c = 0 posee un término de segundo grado, otro de primer grado y un término constante, no podemos aplicar las propiedades de las ecuaciones, entonces, para resolverla usamos la fórmula:

Entonces, las raíces o soluciones de la ecuación cuadrática nos indican los puntos de intersección de la parábola con el eje de las X (abscisas) .

Respecto a esta intersección, se pueden dar tres casos:

Que corte al eje X en dos puntos distintos

Que corte al eje X en un solo punto (es tangente al eje x)

Que no corte al eje X

 Si  a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x ² − 3x − 5

Función cuadrática de Sabrina Dechima